How does one protect AI models and sensitive data in the cloud?
Data-driven analysis and inference involve the use of Machine Learning (ML) and Deep Learning (DL) techniques. These ML and DL functionalities are available in the cloud, and the data owner can use them for decision-making without actually developing the models. However, much of this data is sensitive and poses a security and privacy risk when sharing to the cloud.. Sensitive data, like medical or financial information, needs to be encrypted both at rest and in-transit.
Modern encryption algorithms are virtually unbreakable—at least until the coming of quantum computing—because they require too much processing power to break them. The problem with existing encryption algorithms is that the data needs decryption before processing (for inferencing in ML/DL), which means data is vulnerable to attacks and data privacy can compromised. How can we avoid these risks? Such risks can be avoided if the computation is performed on encrypted data so that the real data is not visible to the processing platform. Is this possible?
Operation on encrypted data is made possible by Homomorphic Encryption (HE).
What is Homomorphic Encryption (HE)?
HE is a lattice-based cryptosystem which allows us to compute on ciphertexts as if we would do them on plaintexts with the decrypted result matching the plaintext operations. Homomorphic refers to homomorphism in algebra with the encryption and decryption functions thought of as homomorphisms between plaintext and ciphertext spaces. HE systems support two operations on ciphertexts viz addition and multiplication (The scheme hides the message in noise. This makes it difficult for other operations to be performed). All other operations can be derived or approximated from these operations. HE schemes can be categorized into three types:
The below figure provides a visual representation for the Homomorphic encryption flow:
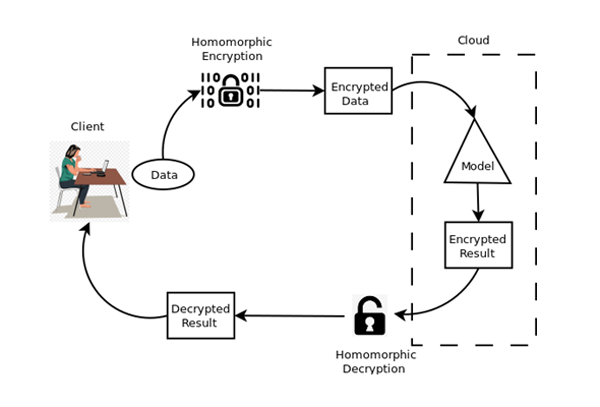
HE provides means to safeguard data as well as the model without leaking any information. HE has been proved to work on inferences of a trained model for different neural network topologies like ANN, CNN, etc. However, many drawbacks need to be considered while using HE in these scenarios.
An alternative to this has been the proposal of differential privacy.
Differential privacy is a property that provides a mathematical guarantee that your privacy is not violated when data is used for analysis. Privacy is preserved by perturbing the original data by adding noise. Usually, a Laplacian or a Gaussian is used as a distribution for noise. DF was initially built with databases and queries in mind. The idea was to compute the usual queries like count, mean, etc. without access to private information. This led to a DF system with two views: one, a global system assumes having a trustworthy aggregator which aggregates data from individuals and adds noise before sending back the result of the query, and two, a local system where noise is added to raw data sending it across to the aggregator that replies to the queries. A magic number epsilon provides the measure of privacy in a DP system. The higher the epsilon, the less the privacy and the more accurate the result. Epsilon can be treated as a privacy loss parameter. Privacy degrades with repeated queries as epsilons add up. A good value is deemed to be between 0 and 1. However, practical implementations have epsilon values greater than 10, which do not serve the purpose of privacy. Local differential privacy works well when we use simple queries like mean count, etc. but can hardly be used for the complex nature of tasks like ML. In those cases, researchers opt for global DP systems where the aim would be to secure the model using techniques like differential privacy—Stochastic Gradient Descent (DF-SGD).
From the above arguments, it is clear that a HE based system would be the most preferred in terms of training ML algorithms. These will protect the data as well as the model. However, HE systems involving ML are practically not ready to be deployed and DP seems to be an attractive alternative. A global DP system would secure the model and ensure security against attacks on raw data. A local DP system perturbing the raw data might severely reduce the model performance (Eg. adding noise to the image might make it unusable to training).
How does HE work in the world of Quantum Computers?
Quantum computers are becoming increasingly popular in providing complex mathematical operations in real-time that would otherwise take several months over a supercomputer. This is possible due to the unique properties of a quantum system, such as the superposition of state and entanglement. New states with the weighted combination of these states will be available for computation. It increases parallelism multi-folds. Entanglement allows similar states to be “braced “together irrespective of their position in space. By creating entangled states, the same operation can be carried out simultaneously over these states. Thus, superposition creates an army, while entanglement weaponizes the same.
While using a quantum computer hosted in the cloud for business solution, two possibilities of encrypting the data exist:
1. Encryption of Quantum states and transfer on to the cloud
This is also referred to as blind quantum computing, as the client is not aware of the encryption keys. The data available with the user is in qubit form, generated by a quantum device and needs to be processed over the quantum computer in the cloud. While the availability of a quantum device at user premises is still a distant dream, the quantum computer over the cloud can still offload a part of its job to another quantum computer over the cloud. For example, the entangled states created by one quantum computer may be classified over another quantum computer that implements the support vector machine. In such a scenario, compromising the data is not possible. The famous “no-cloning theorem” of quantum mechanics says quantum information cannot be duplicated. If it is intercepted, the sender and the recipient will know about it immediately.
The quantum data sender can still go for homomorphic encryption of the data. In this case, the second quantum device does not know what it is processing and maintains the security of the data, which is otherwise impossible.
Still, the transfer of quantum states, encrypted or otherwise, is a major challenge. So far, it has not been possible to transfer the states in bulk beyond the lab premises.
Homomorphic Encryption of normal data and transfer to the cloud
This is similar to the usage of AI models over the cloud except that the models here involve quantum computing. The normal data available on the user devices are subjected to homomorphic encryption and subsequently transferred to the cloud for getting processed by a quantum computer. The method works since the quantum operations are linear and represented by a matrix.
A quantum computer supports fully homomorphic encryption (FHE) algorithm used in classical cryptograp. In a simple implementation, the normal data to be transferred on to the cloud is already encrypted. Quantum states are locally created for this data using a Pauli gate or using a CNOT gate (controlled NOT gate operation supported by a quantum computer). The result is further subjected to quantum operations before providing back to the user. The user can decrypt the result available in classical homomorphic encrypted form and use it.
As an example, consider the data m generated over a classical computing device and required to use a quantum algorithm such as a support vector machine (SVM) classifier. The data needs to be converted into a readable form for the quantum computer before processing starts. This task is accomplished partially by the client device. The remaining part, i.e., creation of quantum states for processing happens on the cloud. The algorithm itself can be realized through a series of quantum gates or transformations, followed by the measurement of the resulting state. Upon analysis, the quantum states so created gets reduced to a classical or real-world bit. These bits may be iteratively taken through the quantum algorithm or provided to the client device as a result.
An integral component of the FHE is the verification of the system. Homomorphic encryption assures data transmission security. However, it does not guarantee the authenticity of the services over the cloud. The service itself may be hacked to return a wrong result to the user. It is required to ensure the integrity of the services provided over the cloud. Classical FHE system compares the log of the processed result for predefined data ingested to the service with the expected result from the cloud. However, such a comparison is forbidden in a quantum system due to the no-cloning principle. As a result, classical cyphertext is generated for the log and decrypted to verify the services' authenticity.
This scheme is realizable for accessing and designing business solutions using quantum computing APIs commercially available over the cloud.
In conclusion, with many applications being deployed in the cloud and the increasing popularity of Quantum computers to solve complex problems, HE and QHE are the way forward to processing without decryption. HE provides encryption by hiding the message in noise, whereas in QHE, encryption is achieved using Pauli gates or randomized phase. As mentioned earlier, FHE is the ultimate prize one looking for as this allows users to share data without inhibition. It holds a lot of promise for a plethora of real-world applications. However, the aim is to find a way to solve the limitations of the technology and make it usable across industries on a larger scale.
References
Manjunath Ramachandra
DMTS Senior member, Principal Consultant
Manjunath has over two decades of experience and works for the CTO Office, Wipro. His areas of interest include the different verticals of signal processing spanning AI, computer vision, etc.
Narendra N
Lead Consultant
Narendra is a Signal Processing and Machine Learning Researcher with more than 9 years of experience.He currently works in the AI Research group at Wipro. His current areas of interest include Homomorphic Encryption, Machine Learning Model Compression, and Bayesian Machine Learning.
Vinutha B N
DMTS Senior Member, General Manager
Vinutha has 25+ years of experience in the embedded space and heads the Wipro CTO AI research team. Vinutha’s interest ranges from understanding the limitations of AI to building transparency in AI to gain human trust and how AI can advance social causes.